Ze Liu∗12, Jia Ning∗13, Yue Cao1†, Yixuan Wei14, Zheng Zhang1, Stephen Lin1, Han Hu1† 1Microsoft Research Asia 2University of Science and Technology of China 3Huazhong University of Science and Technology 4Tsinghua University

---

Abstract

• 지금까지의 video transformer 모델은 globally conntect patches across the spatial and temporal dimensions ⇒ Global에 주목
  • compute self-attention globally even with spatial-temporal factorization
  • ex. ViViT, TimeSformer
• 이 논문에서는 Locality에 주목해서 inductive bias를 활용하고자 함
  • speed-accuracy면에서 더 좋았다
• Swin Transformer 구조를 (그대로) 가져옴

Introduction

• ViT → globally models spatial relationships on non-overlapping image patches with the standard Transformer encoder
  • (original) swin transformer → 모든 patch가 self attention 하는 것에 대한 computation cost를 지적
• ViViT → factorization approach & TimeSformer → factorized self-attention
• Video swin transformer → 위의 모델들보다 더 효율적임을 밝힘
  • inherent spatiotemporal locality를 사용할 수 있음
  • full spatiotemporal self-attention은 locally self-attention으로 approximation될 수 있다
• Swin-Transformer는 inductive bias(for spatial locality)를 사용

Model

Overall Architecture

\[input \ video : T\times H \times W \times 3\]

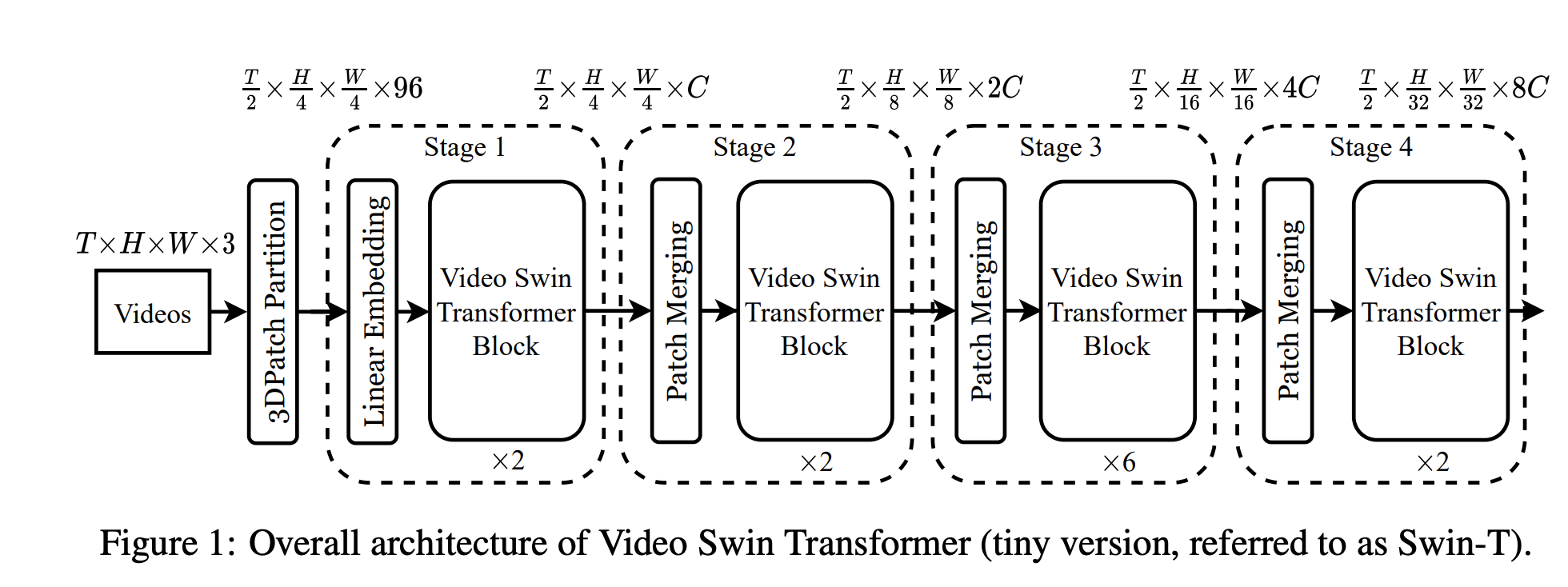
• T : # of frames of video
• 3D Patch Partition
  • 3D patch of size 2x4x4x3 as a token ⇒ 3D patch partitioning layer obtains
  \[\begin{equation} \frac T 2 \times \frac H 4 \times \frac W 4 \end{equation}\]

  3D tokens with each patch/token consisting of a 96-dimensional feature

• Then linear embedding layer → project the features of each token to an arbitrary dimension C
• 전반적인 구조는 오리지널 swin transformer를 따라가고 있음
  • 4 stages로 구성되어 있음
  • 각 스테이지의 Patch merging layer 에서 2x spatial downsampling을 진행함.
    • 패치 개수를 점점 줄이면서 학습함으로써 작은 물체에서 큰 물체까지 모든 정보가 학습될 수 있게 함

• Video swin transformer block

  

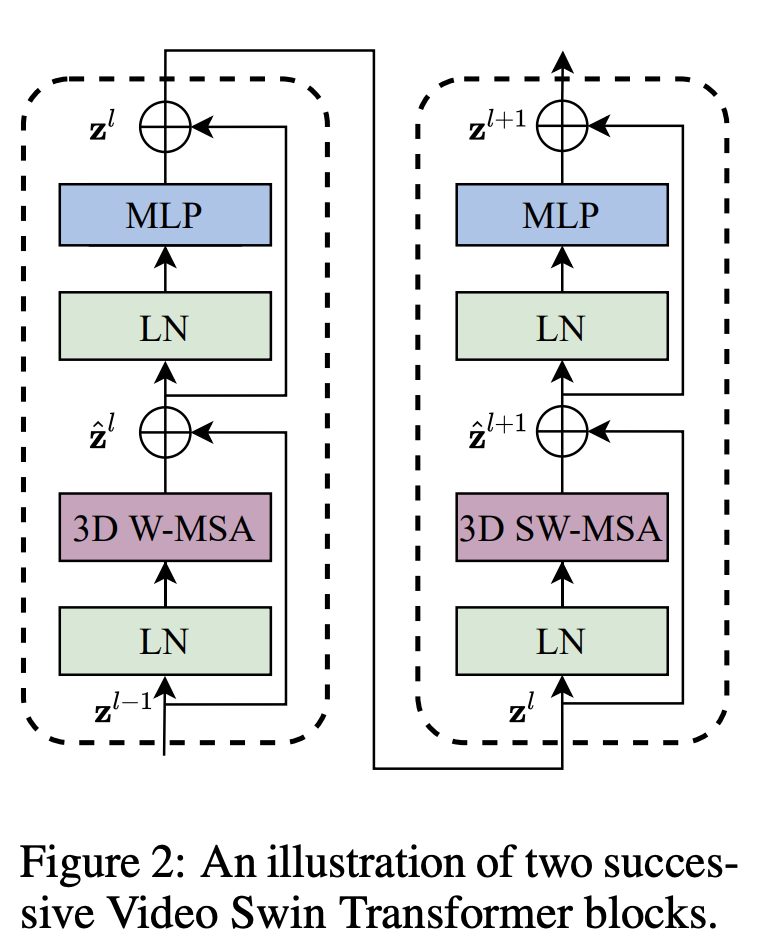
  • 3D shifted window based multi-head self-attention module
  • Layer normalization
  • FF network
    • 2-layer MLP with GELU
  • 각 모듈이 끝나면 residual connection

3D Shifted Window based MSA Module

• Multi-head self-attention on non-overlapping 3D windows
  • Video → T’xH’xW’ 3D tokens 3D window size → PxMxM ⇒ input tokens →
  \[\begin{equation} \lceil \frac {T'} P \rceil \times \lceil \frac {H'} M \rceil \times \lceil \frac {W'} M \rceil \end{equation}\]

  Non-overlapping 3D windows

• 3D shifted windows

  

  

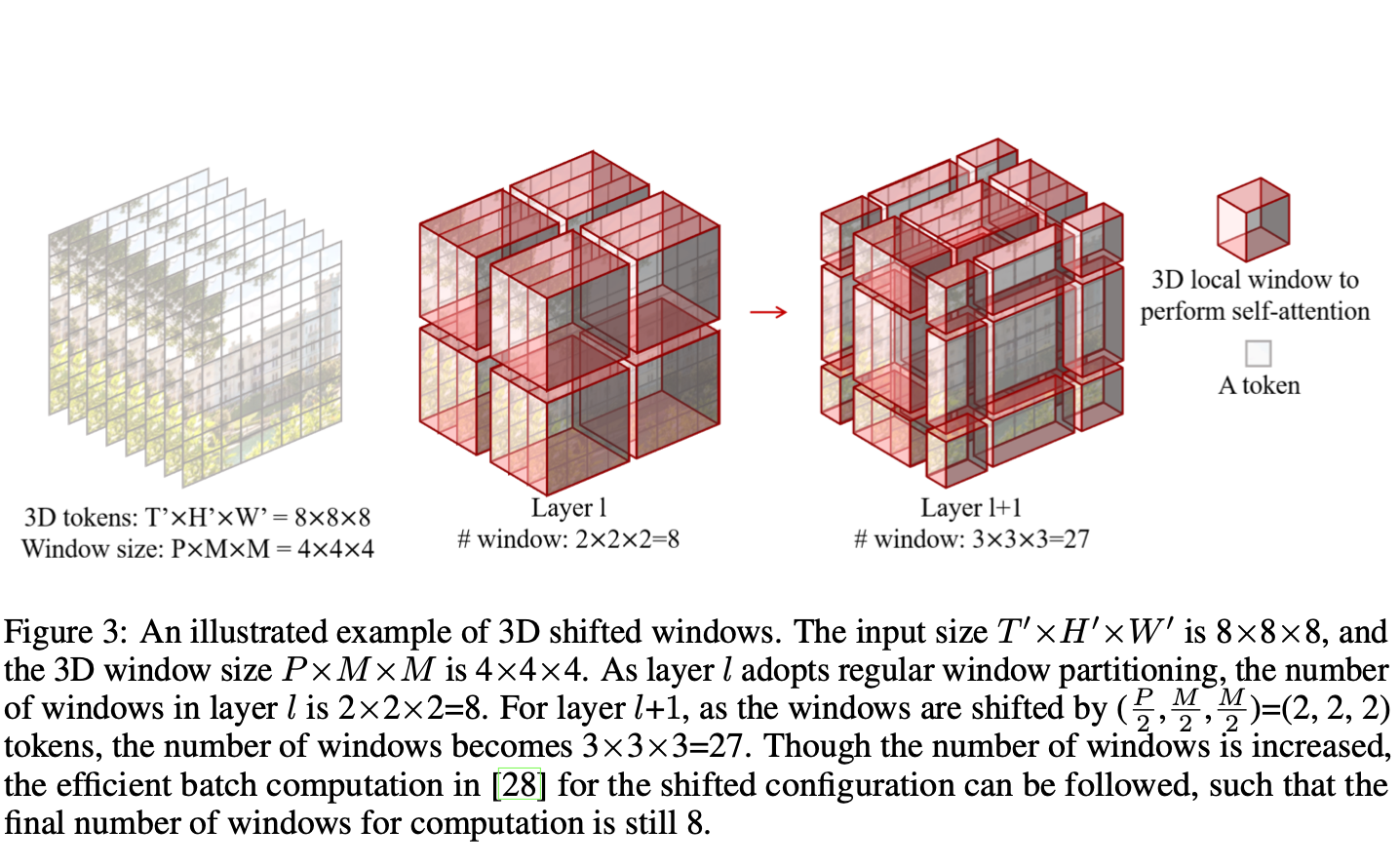
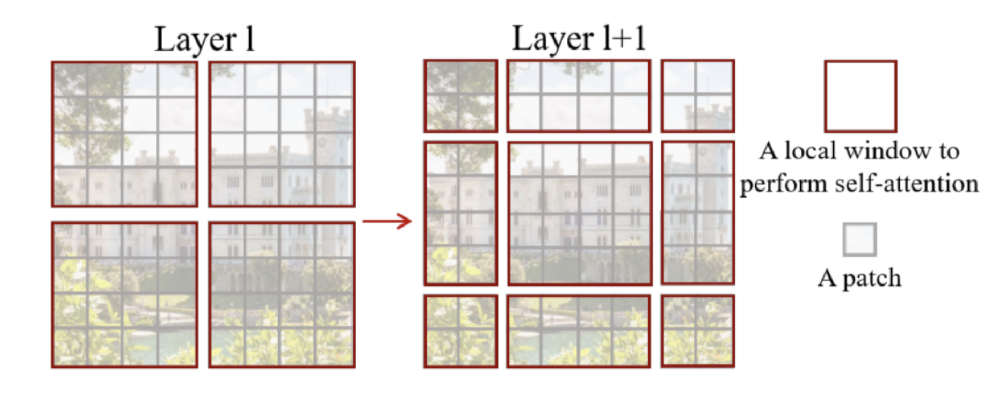
  • Non-overlapping 3D window 각각에 MSA를 적용하면 (== W-MSA) 다른 윈도우 사이의 커넥션 정보가 부족함 → cross-window connections 제안
  • Self-attention module에 2개의 레이어 사용
    • First layer는 “regular window partition strategy” == 앞서 non-overlapping한 3D windows를 사용
    • Second layer는 앞선 레이어에서 shift along the temporal, height, width axes by (P/2, M/2, M/2)한 윈도우를 사용
      • (윈도우 크기의 반만큼 이동)

  • Cyclic shift (FROM original Swin Transformer)

    

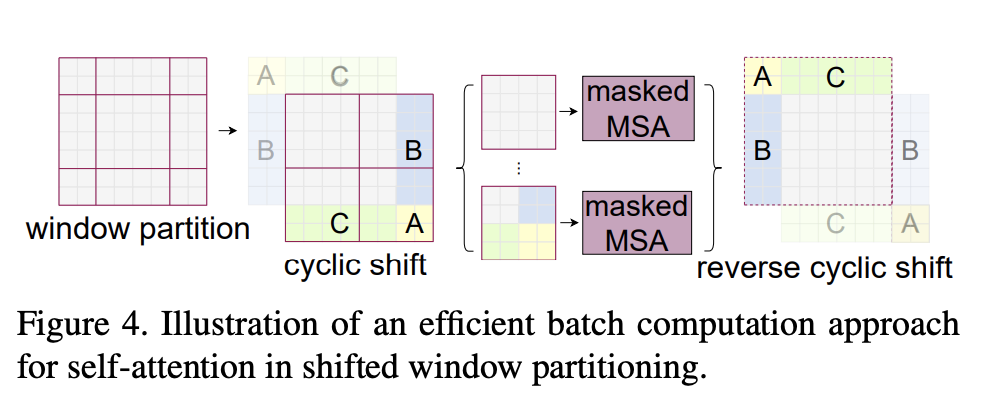
    • 몇몇 윈도우는 mxm 사이즈보다 작을 것임(위 그림에서 4x4가 안되는 것들)
      • Naive solution : padding ⇒ 윈도우 개수가 늘어남
    • 이러한 Sub-window들의 크기를 늘리는 방법이 “cyclic shift”
    • 위의 그림처럼 sub-window(A,B,C)들을 우측 하단으로 이동시켜 window크기에 맞게 합친 뒤 self-attention 계산
      • 윈도우 개수가 늘어나지 않음
      • 새로 붙인 부분들은 인접해있지 않음 → 개별적인 sub-window 내의 attention score를 계산할 수 있도록 masking 기법을 이용한다

• 3D Relative Position Bias

  

  \[\begin{equation} B \in \mathbb{R}^{P^2\times M^2\times M^2} \\ Attention(Q,K,V) = SoftMax(QK^T/\sqrt{d}+B)V \\ Q,K,V \in \mathbb{R}^{PM^2\times d} \end{equation}\]
  • 다른 모델들과 달리 positional encoding역할이 이 블락 안에 있다
    • ViT → q, k, v를 임베딩하기 전에 Positional Encoding
  • 상대 좌표를 이용 → 어떤 픽셀을 중심으로 하냐에 따라서 이동해야 하는 값이 달라지기 때문에 sin, cos 주기를 이용한 절대 좌표보다 더 좋다고 한다 // (original) Swin Transformer

  각 query의 위치를 기준으로 key의 상대적인 위치를 이용해 임베딩을 더해준다

  == 쿼리 기준 키의 상대적인 거리를 얻어서 더해준다

  • Relative poision → the range of [-P+1, P-1] (temporal) or [-M+1, M-1] (height or width) ⇒ parameterize a smaller-sized bias matrix
  \[\begin{equation} \hat{B} \in \mathbb{R}^{(2P-1)\times (2M-1) \times (2M-1)} \end{equation}\]

Experiments

• Dataset
  • Kinetices-400, 600
  • SSv2
• Sample a clip of 32 frames from each full length video using a temporal stride of 2 and spatial size of 224x224 ⇒ resulting in 16x56x56 input 3D tokens (patch size : 2x4x4x3)
• inference (K400, K600)
  • 4x3 views
  • Uniformly sampled in the temporal dimension as 4 clips
    • For each clip, the shorter spatial side is scaled to 224
      • Take 3 crops of size 224x224 that cover the longer spatial axis
  • Final score → average score over all the views
• Inference (SSv2)
  • Window size in temporal dimension = 16
  • 1x3 views
  • Final score → average score over all the views

  

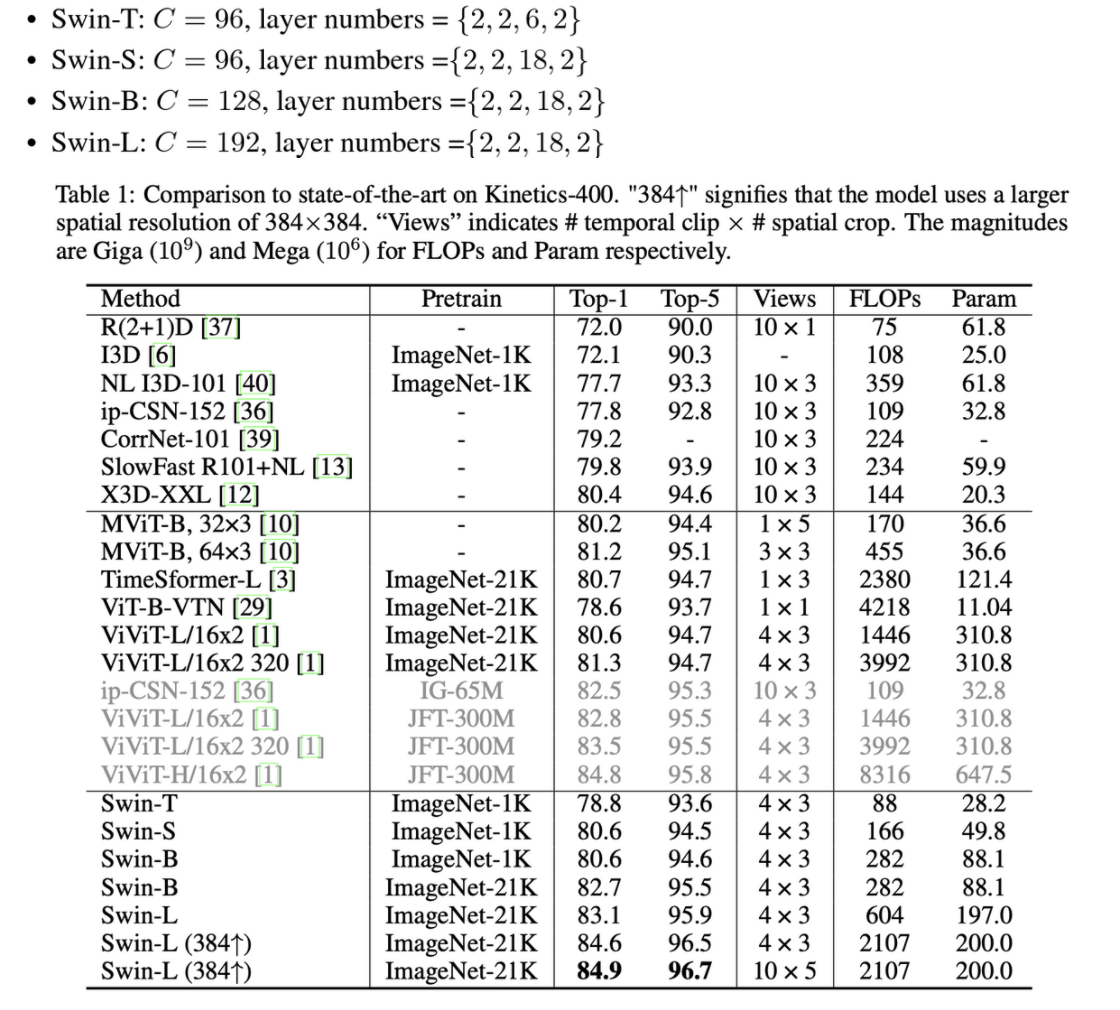
• Ablation Study

  • Temporal dimensions of 3D tokens & Temproal Window Size

    

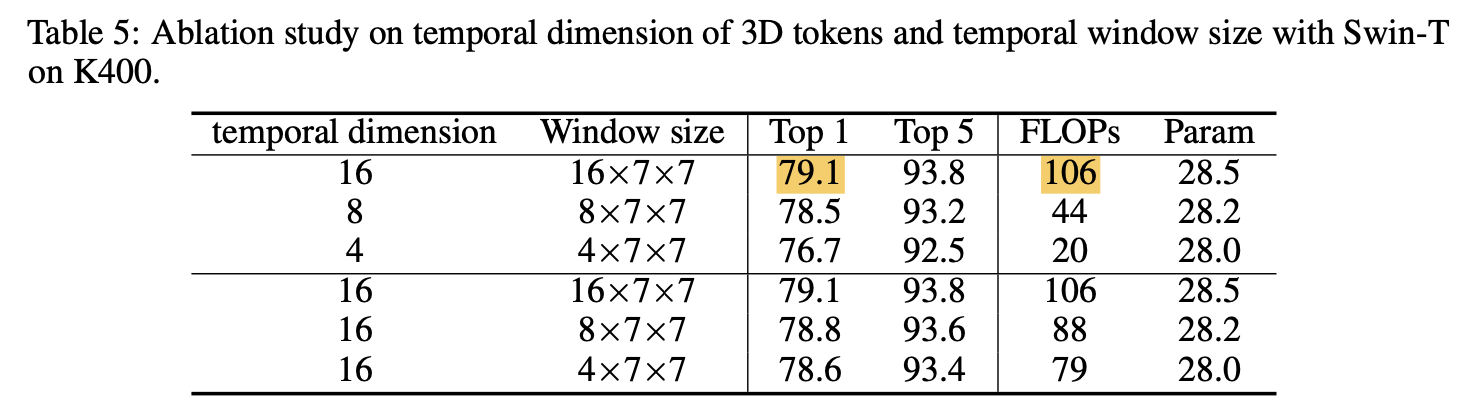
    Temporal dimension이 크면 성능은 좋아지지만 computation cost가 커지고 느려짐

  • 3D shifted Windows

    

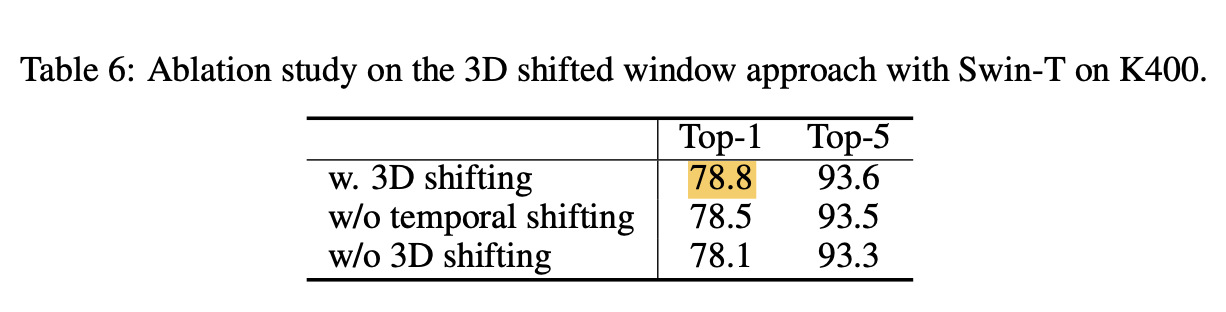
    • 3D shifted window vs. Temporally shifted windwos

---

Summary

• Swin Transformer(vision/image transformer) 구조를 Video model에 적용
• Window 기반의 self-attention 계산 (window 내의 patch들끼리만 self-attn을 한다) → Locality 사용, 계산 복잡도 줄임, inductive bias를 활용한다
  • Video Swin Transformer block → Window MSA, Shifted Window MSA으로 구성
  • 3D Shifted window : 다른 윈도우 사이의 커넥션을 위해 cross window connections 제안
    • Sub-window에 Cylic shift를 사용

Reference

Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

[논문리뷰] Swin Transformer