Object Detection • Object Segmentation • Medical Data • U-Net

U-Net

By VIP-Lab Comment

U-Net

30 July 2021

U-Net: Convolutional Networks for Biomedical Image Segmentation (CVPR, 2015)

https://arxiv.org/abs/1505.04597

  • Semantic segmentation model developed specifically for biomedical images

Motivation

  • use patches to replace the sliding windows
    • reduce redundancy due to overlapping patches
  • large patches → more max-pooling → lower localization accuracy
  • small patches → see only little context

Fully Convolutional Networks

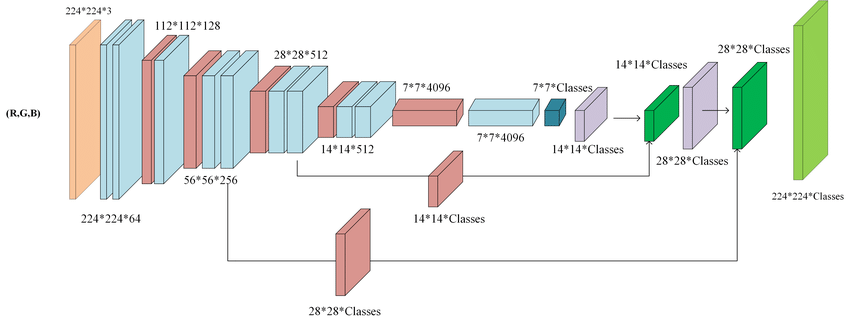
Untitled

  • uses sliding windows
  • remove fully connected layers and replace with $1\times1$ convolution
    • no need to fix the input image shape
    • preserve spatial information
  • skip layers to combine high resolution freatures from the encoder with the upsampled output
    • successive convolution to learn a more precise localization output

Approach

  • upsampling operators with large number of feature channels
    • increase the resolution of the output

    • propagate context information to higher resolution layers

      → U-shaped architecture

  • use patches of the input instead of sliding windows
    • remove redundant computations to reduce the training cost
  • excessive data augmentation
    • learn invariance to deformation of the image corpus
    • learn even with small training set

Network Architecture

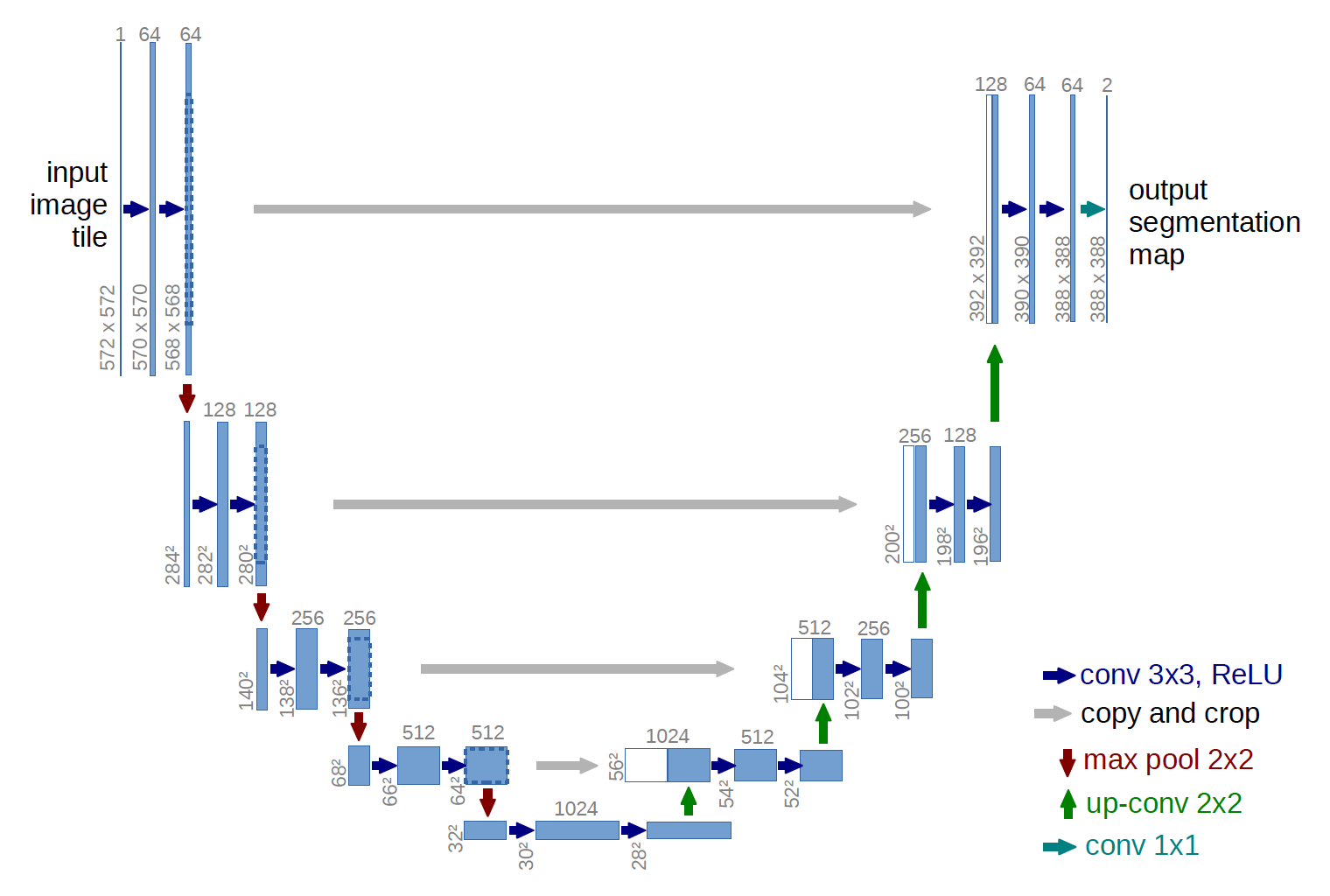
Untitled 1

  • Contracting Path (left half) - encoder
    • repeated $3\times3$ convolutions + ReLU + $2\times2$ max pooling [downsampling]
      • VGG based architecture
    • downsampling: double the number of feature channels
    • convolutions: unpadded

    : extract spatial context using convolutions

  • Expansive Path (right half) - decoder
    • [upsampling] $2\times2$ up-convolution + concat with cropped feature map + $3\times3$ convolutions + ReLU
    • upsampling: halve the number of feature channels
    • concatenation: skip connection between encoder and decoder → combine context information to localization step to enhance pixel segmentation
      • cropping: necessary due to the loss of border pixels in every convolution
        • unpadded convolution → different input & output size (572572 & 388388): missing border pixels
        • solution 1) mirror extrapolation
          • extrapolate the missing context by mirroring the input image instead of zero-padding

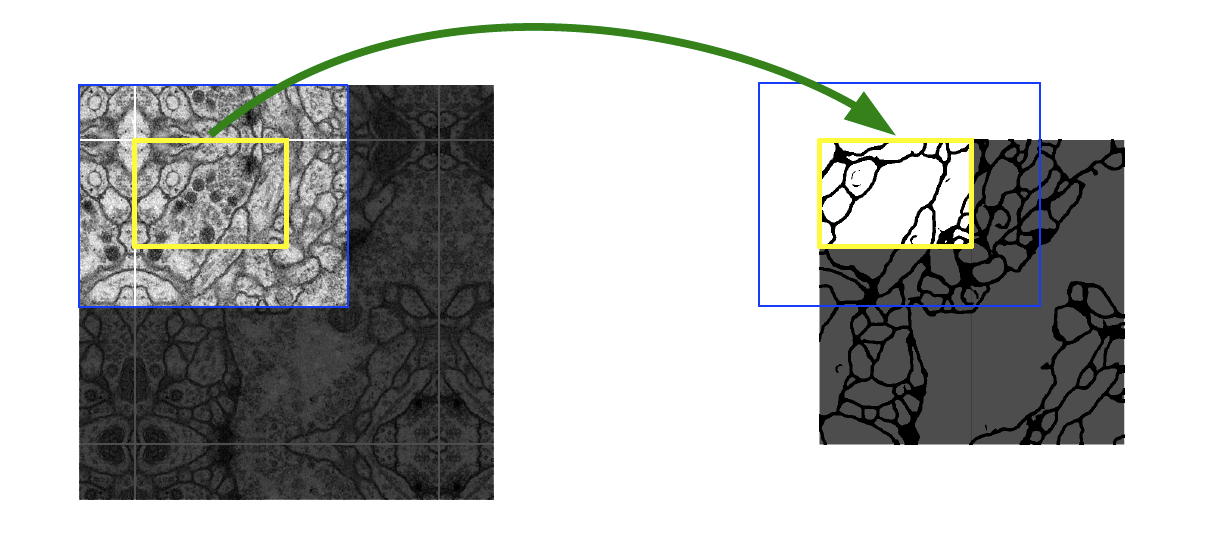
          Untitled 2

        • solution 2) overlap-tile strategy
          • generate seamless segmentation that only pixels for which the full context is available from the input image
          • important to apply to large images (by separating the original input into overlapping tiles)

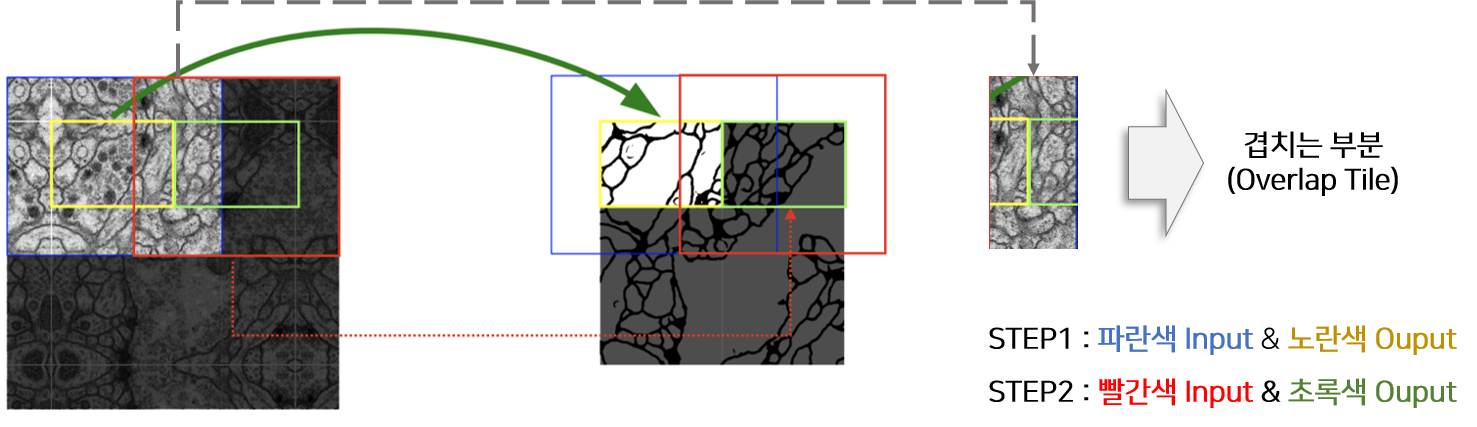
          Untitled 3

    : increase localization accuracy by using both upsampled information and context feature map

  • final layer
    • $1\times1$ convolution: map each component feature vector to number of classes
      • classification without FC layer to preserve spatial information

Training

  • implementation: SGD of Caffe
  • to minimize overhead: large input tiles over a large batch size → reduce batch to a single image
  • loss: pixel-wise soft-max function combined with cross entropy
    • pixel-wise soft-max
      • $p_k(x):\text{ probability that pixel }x \text{ belongs to class }k$
      • $a_k(x): \text{logit that pixel }x \text{ belongs to class }k$ (model output)
    \[p_k(x)=\exp(a_k(x))/(\Sigma_{k'=1}^K\exp(a_{k'}(x))\]
    • cross entropy loss
      • penalize each pixel if $p_{l(x)}(x)$ deviates from 1
        • $p_{l(x)}(x) =1 \text{ if pixel }x \text{ belongs to class }l(x)$
        • $l(x): \text{GT label of pixel }x$
    \[E=\sum_{x\in\Omega}w(x)\log(p_{l(x)}(x))\]

    • weight map

      Untitled 4

      • large if pixel x is close to the borders → more weight for border adjacent pixels
      • $w_0, \sigma: \text{hyperparameters; by defualt: } 10, 5$
      • $w_c(x): \text{weight map to balance the class frequencies}$
        • more weight to less frequent labels → learn even the segments of small area
      • $d_1(x): \text{pixel }x’s \text{ distance to the border of the nearest cell}$
      • $d_2(x): \text{pixel }x’s \text{ distance to the border of the second nearest cell}$
    \[w(x)=w_c(x)+w_0 \cdot\exp(-\frac{(d_1(x)+d_2(x))^2}{2\sigma^2})\]
    • pre-computed weight map for each ground truth segmentation: compensate different frequency of pixels from a certain class in the training sset → force the network to learn small separation borders

  • Why weight loss?

    → proportion of border pixels is low: without weight loss, borders between different objects that belong to the same class might be ignored and displayed as a single object

Experiments

  1. segmentation of neuronal structures [EM segmentation challenge]
    • warping error: segmentation metric, cost function for learning boundary detection
    • rand error: defined as 1 - the maximal F-score of the foreground-restricted Rand index, measure of similarity between two clusters or segmentations
    • pixel error: squared Euclidean distance between the original and the result labels

    Untitled 5

  2. light microscopic images [ISBI cell tracking challenges]
    • IOU results (intersection over union)

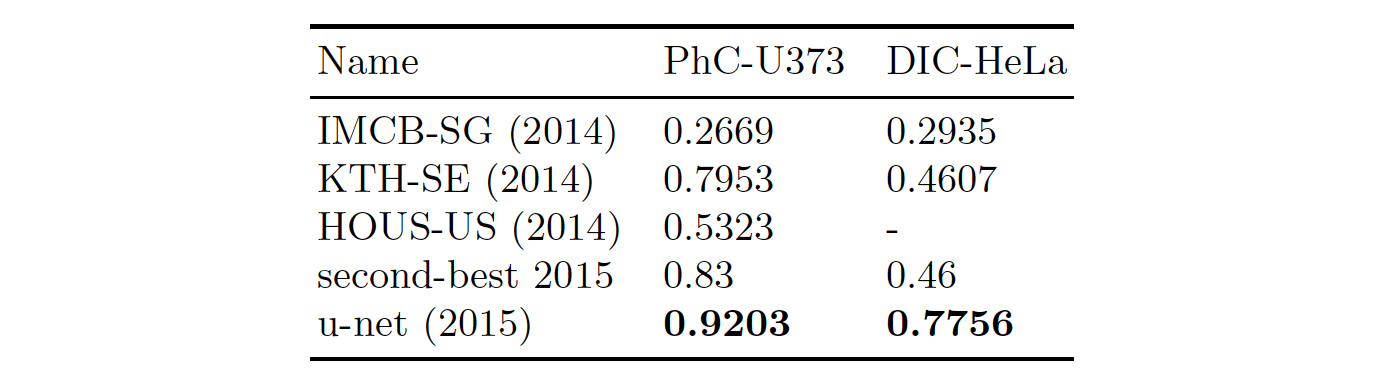
    Untitled 6

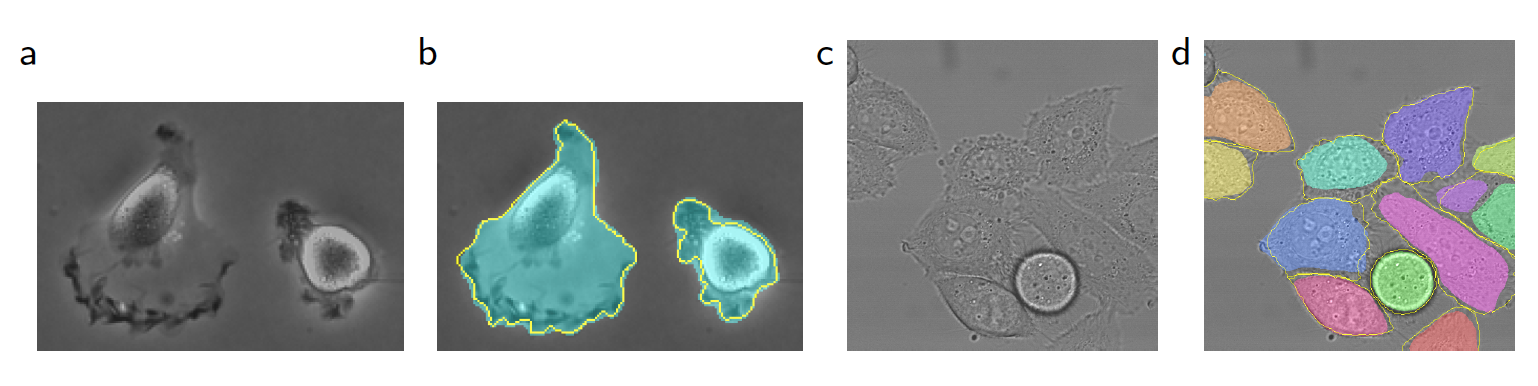
    • segmentation results

    Untitled 7

Contributions

  • faster training speed
  • optimize trade-off between good localization and the use of context

References

  1. https://arxiv.org/abs/1505.04597
  2. https://joungheekim.github.io/2020/09/28/paper-review/
  3. https://kuklife.tistory.com/119