Non-local Neural Networks
15 July 2021
Non-local Neural Networks (CVPR, 2018)
long-distance dependencies
modeled by large receptive fields formed by deep stacks of convolutional operations
local operations (convolutional, recurrent operations)
- computationally inefficient
- optimization difficulties
- difficult multi-hop dependency modeling
- → Non-local operations to capture long-range dependencies
-
RNN/CNN 모델 자체에 내재되어 있는 한계점 존재
Non-local operation
- classical non-local mean operation in CV
: weighted sum of features at all positions in the input feature maps

position $X_i$ 의 response 값을 계산할 때 모든 position $X_j$의 weighted average로 계산
- weight는 픽셀 간의 similarity로 계산, ex) euclidian distance of gray level vectors
(위 사진에서는 값이 큰 포지션만 보여짐, 이런 방식으로 frame 1과 frame 3, 4의 축구공 간의 관계가 강조됨)
- 노이즈 제거에 있어서 주변 영역만이 아니라 이미지 전체에서 유사한 부분을 찾아서 활용하는 방식
position: can be in space, time, or spacetime → applicable for image, sequence, video problems
advantages
- can capture long-range dependencies directly by computing interactions between any two positions
- efficient only with a few layers
-
maintain the variable size → can be easily combined with other operations (ex. convolutions)
: used as a generic family of building blocks for capturing long-range dependencies
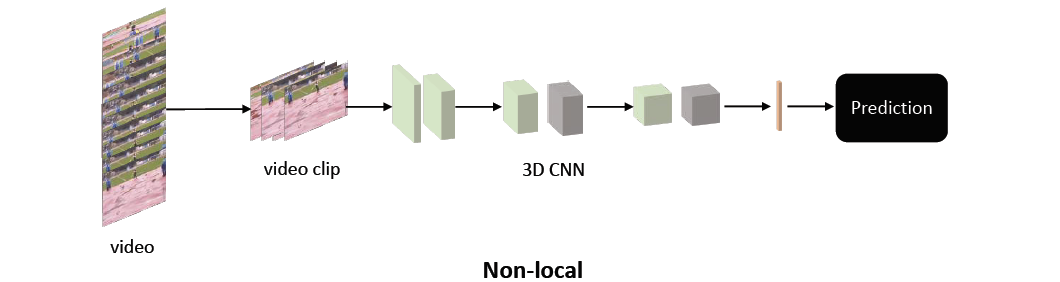
- self-attention can be viewed as a form of the non-local mean
Methodology
\[y_i = \frac{1}{C(x)}\sum_{\forall j}f(x_i, x_j)g(x_j)\]- $g(x_j)=W_gx_j$: linear embedding with a learned weight matrix
- $f(x_i, x_j)$
- Gaussian: $f(x_i, x_j)=e^{x_i^Tx_j}$
- Embedded Gaussian: $f(x_i, x_j)=e^{\theta(x_i)^T\phi(x_j)}$
- Dot product: $f(x_i, x_j)=\theta(x_i)^T\phi(x_j)$
- Concatenation: $f(x_i, x_j)=ReLU(w_f^T[\theta(x_i), \phi(x_j)])$
- Non-local block
residual connection $x_i$: can insert non-local block to any pre-trained model without breaking initial behavior
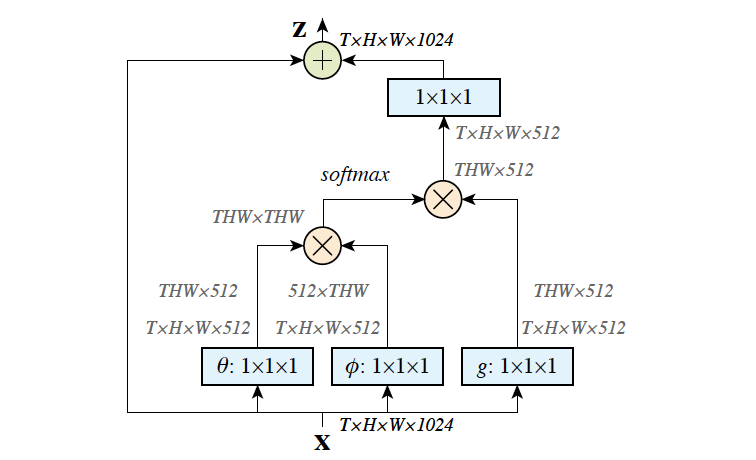
ㄴ residual block of embedded gaussian $f(x_i, x_j)$
Experiments
models
baseline 1) C2D (2D ConvNet baseline)
- ResNet-50 backbone
- 2D kernels, temporal dimension addressed only by pooling
baseline 2) I3D (Inflated 3D ConvNet)
- inflate 2D kk kernels as 3D tk*k kernel that spans t frames
→ add 1, 5, or 10 non-local blocks to each baselines for non-local networks
datasets
Kinetics
- 246K training, 20K validation, 400 human action categories
results
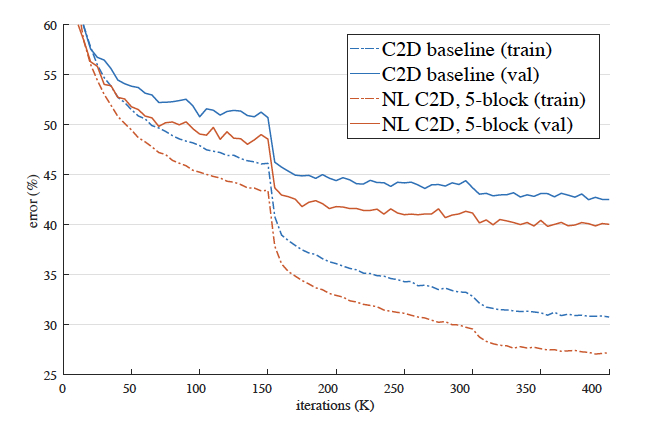
- ablation studies
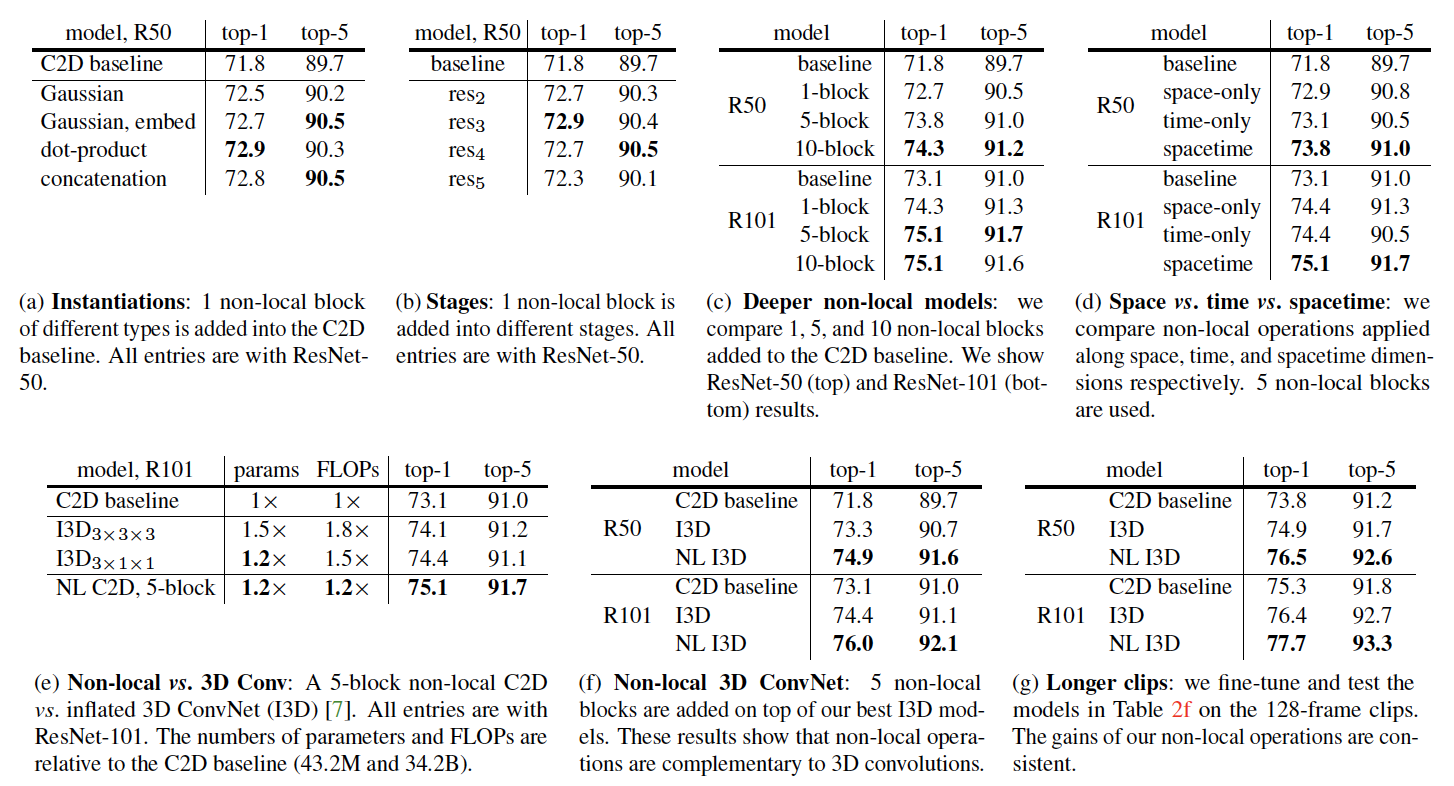
- aggregation 방식
- Embedded Gaussian / Dot-product / Concatenation이 효과적, 주로 Embedded Gaussian 활용
- non-local block을 추가할 위치
- stage가 뒤에 있을수록 효과적인데, 가장 마지막 stage (res5)에서는 이미 정보 손실이 너무 많이 일어나서 효과가 상대적으로 적다고 추정
- layer의 개수
- NL block을 더 많이 쌓을수록 성능 향상
- 시간 vs 공간 vs 시공간
- 시간: 여러 frame의 같은 position에 대해서만 aggregate
- 공간: 한 frame 안에서만 aggregate
→ 시공간 모두를 계산하는 방법이 가장 효과적
- 기존 SOTA와의 성능 비교
- NL block을 추가한 버전이 더 효과적
- depth별 성능 비교
- ResNet 기준, 더 깊은 레이어의 ResNet101이 더 효과적
→ 즉, long-term dependency 문제를 잘 해결했음
- long-distance에의 성능
- 극단적으로 frame의 길이를 더 늘렸을 때도 좋은 성능 보임
Conclusion
- 기존 two-stream networks에서처럼 optical flow를 사용하여 motion을 탐지하지 않고, RGB 값만을 활용한 적은 계산량으로도 non-local 정보를 통해 좋은 성능을 달성
- Non-local block은 네트워크의 구조가 아니라 building block의 형태이고, 차원을 유지하며 residual을 더해주면서 기존 operation의 작용을 방해하지 않기 때문에 유연하고 독립적으로 레이어의 여러 위치에 추가할 수 있음
- 기존의 효율적인 pretrained network의 중간에 추가했을 때 효과적
