Alias Free GAN (Technical Details)
[0] Motivation
-
Careless Model Design → Amplifying Aliasing → Texture Sticking

-
Goal: “An architecture that exhibits a more natural transformation hierarchy, where the exact sub-pixel position of each feature is exclusively inherited from the underlying coarse features.”
[1] Signal Processing Basics
- Sampling
-
Continuous Signal → Discrete Signal
$s_c(nT) = s_d[n]$
$T$: Sampling Period
-
-
Fourier Transform

- Decomposition of a signal
-
Transformation between time domain and frequency domain
(Fourier Transform)
(Time → Freq) $S(f) = \int_{-\infty}^{+\infty}{s(t)e^{-j 2\pi ft}dt}$
(Freq → Time) $s(t) = \int_{-\infty}^{+\infty}{S(f)e^{j 2\pi ft}df}$
(Discrete Time Fourier Transform)
(Time → Freq) $S(f) = \sum\limits_{n=-\infty}^{+\infty}{s(n)e^{-j 2\pi fn}}$ *cf. $S(f)=S(f+1)$
(Freq → Time) $s(n) = \int_{-\pi}^{+\pi}{S(f)e^{j 2\pi fn}df}$
⇒ $s(t)=\sum\limits_i{A_ie^{j2 \pi f_it}} \; \leftrightarrow \; S(f)=\sum\limits_{i}{A_i\delta(f-f_i)}$
*Representation becomes much more simpler!
- Property
- Sinc Function (time) $\stackrel{\mathrm{FT}}{\longleftrightarrow}$ LPF (freq)
- Convolution($\ast$) $\stackrel{\mathrm{FT}}{\longleftrightarrow}$ Multiplication($\cdot$)
- Low Pass Filtering (LPF)
-
Sinc Function (time) $\stackrel{\mathrm{FT}}{\longleftrightarrow}$ LPF (freq)
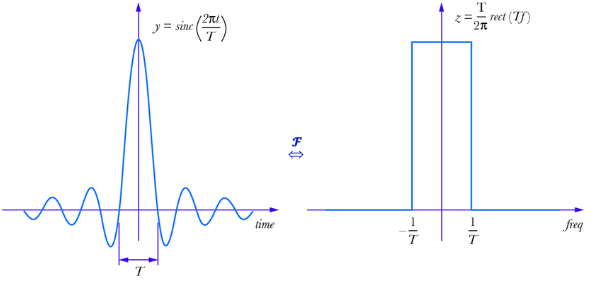
-
Recovering (original) continuous signal from (sampled) discrete signal could be done w LPF
$S_d(f) \xrightarrow{LPF} S_c(f)$
-
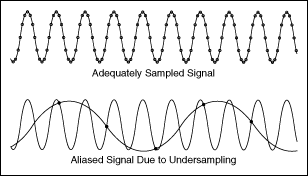
- Aliasing
- Q. Could we recover full original signal from sampled signal?
-
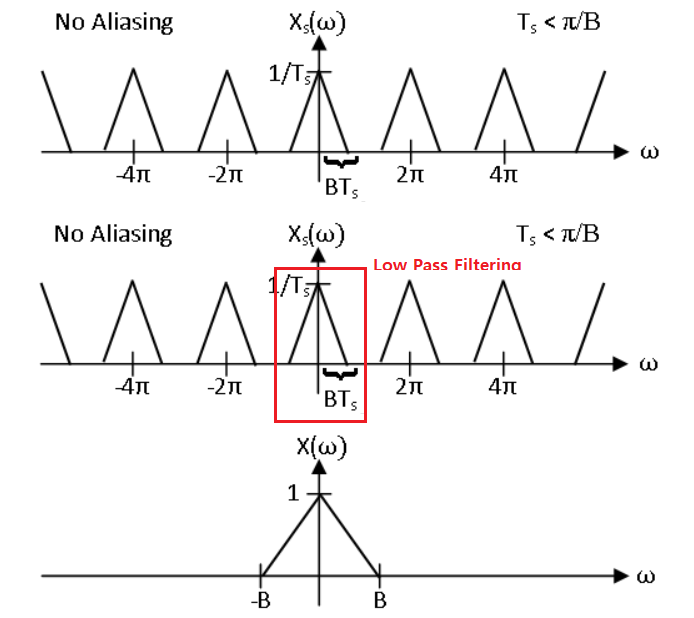
Nyquist Theorem
if, $f_s \geq 2f_m$ → Original signal could be fully recovered!
($f_s$ : Sampling ratio / $f_m$: Original signal frequency)
(Intuitively)
- It’s just impossible to guess original information with very sparse hints!
(Mathematically)
-
$s_c(nT_s) = s_d[n]$
$S_d(f) = \frac{1}{T_s}\sum\limits_{n=-\infty}^{+\infty}{S_c((f-n)/T_s)}$Let’s say, $S_c(f)=0$ for all $|f| \geq f_m$
If, $f_s\leq 2f_m$, Then, $S_c((f-n)/T_s)$ would be overlapped among different $n$s Which means original signal is harmed by sampling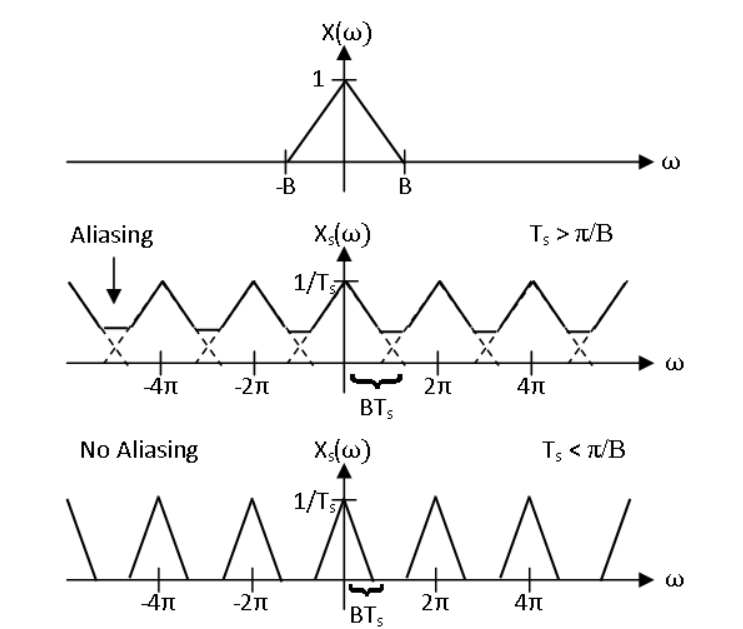
- Impulse Response / Frequency Response
-
System
$O(f)=H(f)I(f) \leftrightarrow o(t)=h(t) \ast i(t)$
($i(t)$ : Input Signal / $h(t)$ : System (= Transfer Function) / $o(t)$ : Output Signal) -
Impulse Response / Frequency Response
-
Impulse Response
:= $o(t)$ when $i(t)=\delta(t)$ → $O(f)=H(f)D(f)=H(f)$ → $o(t)=h(t)$
-
Frequency Response
:= $H(f)$
-
-
[2] Model
- Structure
- Backbone: StyleGAN2
- Goal: To make every layer equivariant w.r.t. the continuous signal
- So that all finer details transform together with the coarser features of a local neighborhood
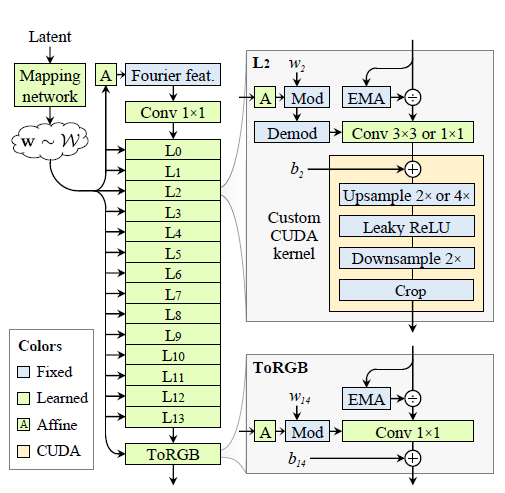
- But, Removed some details
- per-pixel noise
- mixing regularization
- path length regularization
- output skip connection
- Replaced input to Fourier Feature to facilitate exact Translation&Rotation
-
$\gamma(\textbf{v})=[cos(2\pi\textbf{Bv}),sin(2\pi\textbf{Bv})]^{\rm{T}}$
-
- Goal: To make every layer equivariant w.r.t. the continuous signal
- Backbone: StyleGAN2
- Image as a Signal
-
Image is a two-dimensional sampled signal *Each pixel → Sample *# of pixels along axis → Sampling Ratio
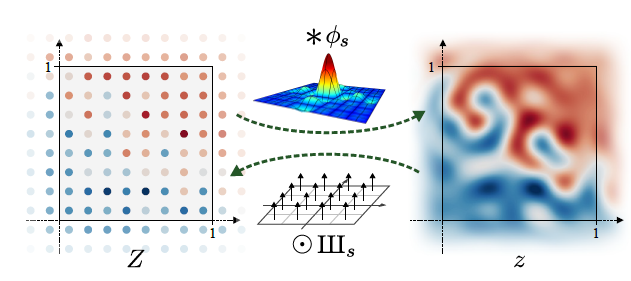
- $Z \xrightarrow{LPF}z$
- $Z$ should be unlimited
- It’s impractical!
- Storing slightly larger than the unit square is practically enough!
- Chose 10-pixel margin
- For a discrete operation $\textbf{F}$
-
Corresponding continuous operation $\textbf{f}$ exists
s.t. $\textbf{f}(z) = \phi_{s’} \ast \textbf{F}(\Pi_{s} \odot z) \; \longleftrightarrow \; \textbf{F}(Z) = \Pi_{s’} \odot \textbf{f}(\phi_{s} \ast Z)$
- In the latter case, $\textbf{f}$ must be bandlimitted to $s’/2$
-
-
- Anti-Aliasing Processing
- Equivariance
- if, $\textbf{f} \circ \textbf{t} = \textbf{t} \circ \textbf{f}$ → $\textbf{f}, \textbf{t}$ are equivariant
- Successful Anti-Aliasing → Sub-pixel Equivariance to Translation, Rotation for all layers
-
Per-layer operations
Per-layer processing in StyleGAN2 contains Convolution, Upsampling&Downsampling, Nonlinearity
→ They are preferable to satisfy Bandlimit, Equivariance to Translation and Rotation
- Convolution
-
$\textbf{F}_{conv}(Z) = K \ast Z$
$\longleftrightarrow \; \textbf{f}_{conv}(z) = \phi_{s} * (K*(\Pi_{s} \odot z)) = K * (\phi_{s} * (\Pi_{s} \odot z)) = K \ast z$*Convolution($\ast$) is commutative
-
To Check
- Bandlimit → introduce no new freq. (Same!) → OK
- Equivariance to Translation of $\textbf{f}$ → trivially fulfilled! → OK
- Equivariance to Rotation of $\textbf{f}$ → $K$ should be radially symmetric (e.g. 1x1 conv)
-
- Upsampling&Downsampling
- Upsampling
-
$\textbf{f}_{up}(z)=z$ $\longleftrightarrow \; \textbf{F}_{up}(Z)=\Pi_{s’}\odot (\phi_{s}*Z)$
- Ideal upsampling doesn’t change anything in the $z$
- Replaced bilinear upsampling module in the model to LPF (windowed sinc function (not jinc.. why..?))
-
- Downsampling
-
$\textbf{f}_{down}(z) = \psi_{s’} \ast z$ $\longleftrightarrow \; \textbf{F}_{down}(Z)=\Pi_{s’}\odot (\psi_{s’} \ast (\phi_{s} \ast Z))=(s’/s)^2\cdot \Pi_{s’}\odot (\phi_{s’} \ast Z)$
($\psi_{s}=s^2\cdot \phi_{s}$ (normalized $\phi_{s}$ to unit mass))
-
To Check
- Bandlimit → Need LPF to $s’/2$ before discretization
- Equivariance to Translation of $\textbf{f}$ → trivially fulfilled! → OK
- Equivariance to Rotation of $\textbf{f}$ → $\phi_{s’}$ should be radially symmetric (e.g. jinc function)
-
- Upsampling
- Nonlinearity (e.g. ReLU)
-
$\textbf{f}_{\sigma}(z)=\psi_{s} \ast \sigma(z)=s^2\cdot\phi_{s} \ast \sigma(z)$ $\longleftrightarrow \textbf{F}_{\sigma}(Z)=s^2\cdot \Pi_{s}\odot(\phi_{s} \ast \sigma(\phi_{s} \ast Z))$
-
To Check
- Bandlimit → Need LPF whose bandlimit of $s/2$ before discretization (Nonlinearity introduces offending high-frequency contents)
-
Equivariance
$\textbf{F}_{\sigma}(Z)$ contains operations in continuous domain
→ pseudo-continuous representation is needed!
e.g. Upsampling → Nonlinearity → Downsampling (2x Upsampling was sufficient)
→ It’s inefficient in CUDA → Implemented custom CUDA kernel (10x faster)
- Equivariance to Translation of $\textbf{f}$ → trivially fulfilled! → OK
- Equivariance to Rotation of $\textbf{f}$ → $\phi_{s}$ for downsampling should be radially symmetric (e.g. jinc function)
-
- Convolution
- Equivariance
- LPF
-
Ideal LPF : impractical
(Due to it has infinite impulse response ; sinc function)
- Implementation Inefficiency
- Border Artifacts
- Ringing Artifacts
-
Kaiser Filter : practical LPF (FIR)
(1D) $h_K(x) = 2f_c \cdot sinc(2f_cx) \cdot w_K(x)$
(2D) $h_K^{\circ}(\textbf{x})=(2f_{c})^2\cdot jinc(2f_c||\textbf{x}||)\cdot w_K(x_0)\cdot w_K(x_1)$$w_K(x)$: window function
- Should lower the cutoff freq. (It’s non-ideal!)
- $f_c=s/2-f_h$
- Should lower the cutoff freq. (It’s non-ideal!)
-
- Model Configurations
- Config T (EQ-T: 45.2 → 63.01)
- Strongly attenuate near bandlimit
- Increased $f_h$ in the lowest resolution layers
- Attenuation: 42dB → 480dB
- But, didn’t do it in the highest resolution layers
- To preserve details (high-freq.)
- Increased $f_h$ in the lowest resolution layers
- Strongly attenuate near bandlimit
- Config R (EQ-R: 13.12 → 40.48)
- It performs the best. But..
- Slow
- Sensitive to hyperparams
→ [Config T] would be better in practical usage
- Replaced 3x3 conv → 1x1 conv (radially symmetric)
- While doubling # of feature maps together
- sinc LPF → jinc LPF
- Didn’t do them in the highest resolution layers
- To preserve details (non-radial spectrum)
- It performs the best. But..
- Config T (EQ-T: 45.2 → 63.01)
[3] Metrics
-
PSNR (Peak Signal to Noise Ratio)
~ $\mathbb E(\frac{{max(Ref. Signal)-min(Ref.Signal)}^2}{Mean{[Ref.Signal-Approx.Signal]^2}})$
-
Equivariance
~ $PSNR(\textbf{t}[\textbf{G}(z_0;\textbf{w})], \textbf{G}(\textbf{t}[z_0];\textbf{w}))$
*Expectation was calculated with 50,000 of random sample points- EQ-T
- $\textbf{t}$ → Translation
- EQ-R
- $\textbf{t}$ → Rotation
- EQ-T
-
FID (Frechet Inception Distance)
[4] Result

- Seems AFG invented a “Coordinate System” inside..!
- Which allows precise localization “on the surfaces”
[5] Future Work
- Anti-Aliasing Processing for Discriminator
- Re-introduce noise inputs, path length regularization of StyleGAN2 in a better way
